Trigonometric Derivatives - Part 3: Arcsine, Arccosine, Arctangent

Problem: We have found 6 of the trigonometric derivatives. And now, we need the last 3. 

After doing 6 of these, we'd expect them to get easier, because of practice. That is just not the case. Because these are inputting the ratios and extracting the angles, these aren't as easy as the others. We're going to have to look at a triangle and try to understand exactly what we're doing.

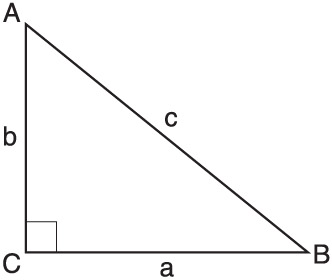
So we're going to look at angle B. The following statement is true:

sin(B)=b/c

However, we want this thing in terms of x. So I'm going to set b/c=x, and B=y, just for the sake of using x and y.

Because sin(y)=x, arcsin(x) must be y as well.

So we will find the derivative of sin(y)=x with respect to x.

By taking the derivative, sin(y) becomes cos(y), but there is a chain rule within this, so we multiply by the derivative of the inside (which is y'). And the derivative of x is 1. The derivative is now y', so we should solve for that.

Now the issue becomes: We need this in terms of x, since that's what the derivative is all about. However, we can't just plug in arcsin(x) for y, or it just looks bad. So I'm gonna rewrite cos(y) in terms of sine. We can do this using the following trigonometric identity:

sin²(x)+cos²(x)=1

We can get the following statement:

Then we can substitute arcsin(x) for y, and simplify to find that the derivative of arcsin(x) is:

Next, we can apply a similar tactic to arccosine. In fact, I'm realizing it's the exact same situation, except because the derivative of cos(x) is -sin(x), the derivative is just going to be mirrored across the x-axis, which is proven here.

I used a program called "MathType" to speed up the process. That's why the fractions look the way they do. I would have changed it, but I don't exactly know how, and I'm not quite willing to find out right now.

Now, I have to find the derivative of arctan(x), which is the last one. Luckily, it follows the same rules.

This is what I have so far, but now I have to write this in terms of tan(y). Looking at it, it actually seems intimidating at first, but it's actually quite simple. Because cos(x)=1/sec(x), we can use a trigonometric identity here. 

Now, we just have to get this in terms of x, which shouldn't be difficult, considering tan(arctan(x))=x.

And there we go! Now we have the trigonometric derivatives of sine, cosine, tangent, cosecant, secant, cotangent, arcsine, arccosine, and arctangent.

Trigonometric Derivatives - Part 2: Cosecant, Secant, Cotangent

Problem: We now have the derivative of sine, cosine, and tangent. Now we have the next set to find derivatives for.

If you haven't already read part 1, go ahead and read all about it here. If you have, go ahead and continue.

We now have the basic trigonometric derivatives.

Original -> Derivative

sin(x) -> cos(x)

cos(x) -> -sin(x)

tan(x) -> sec²(x)

Next, we need to find it for csc(x), sec(x), and cot(x). Luckily, this shouldn't take long, since they're all quotient rules, which was explained in the previous blog (the link is above). So we can easily apply them to these.

The next step will look weird, only because the value of 1 is in the numerator. Its derivative is 0, removing the first half of the derivative's numerator.

And finally, we can simplify.

Once again, that's a lot nicer than I thought. Next, we will find the derivative of sec(x), which should work out in a similar fashion.

This makes sense, considering the derivative of cos(x) makes us subtract a negative from 0, entering the positive realm. And because sin(x) was in the numerator and cos(x) in the denominator, it makes sense that tan(x) was the result instead of cot(x).

And finally, let's solve for the derivative of cot(x). 

I saw this, and for some reason thought it looked like it would be a pain. But really, we just end up with -1 in the numerator.

This is great! We have now found 6 of the trigonometric derivatives!

sin(x) -> cos(x)

cos(x) -> -sin(x)

tan(x) -> sec²(x)

csc(x) -> -csc(x)*cot(x)

sec(x) -> sec(x)*tan(x)

cot(x) -> -csc²(x)

In the next blog post, we will find the derivatives of arcsin(x), arccos(x), and arctan(x).

Trigonometric Derivatives - Part 1: Sine, Cosine, Tangent

Problem: We have 9 trigonometric functions: sin(x), cos(x), tan(x), csc(x), sec(x), cot(x), arcsin(x), arccos(x), arctan(x). We want to find their derivatives in some way or another. In this first part, I will be going over the main 3.

Last class, my teacher explained "Even though we have 9 more derivatives to learn, all it takes is one, and we can easily find the rest. In this blog post, I will hopefully be finding all the derivatives. To start off, I will be finding the derivative of sin(x) using First Principles. For those who don't know what First Principles are, here's what it is.

For those who are new to calculus, welcome. The derivative is the instantaneous rate of change of a function. If you try to use the regular slope formula (rise over run), you'll get 0/0. So rather than using the same points, we're going to take two points and move one infinitely close to the next, hence the limit as ∆x approaches 0. But for the purposes of this, I will be setting h = ∆x.


So f(x)=sin(x). We'll substitute this in, and end up with the following.

Next, we'll use the trigonometric identity of sin(x+h) = sin(x)*cos(h)+cos(x)*sin(h).

The next step is to split this into three fractions, and therefore three limits.

Next, we can use another trigonometric identity on the second limit, which states that the quotient of sin(x) and x as x approaches 0 is 1. Next, for simplicity, I'm actually going to combine the remaining limits, as we will be able to see another identity.

Next, we can apply the distributive property in reverse. 

And finally, the limit as h approaches 0 is equal to 0, which is easily shown on a graph.

I realize after all this, that I haven't been using proper notation. I should have an f'(x) behind each of those. However, I will not spend more time fixing this, as each of those is an image that I would have to remake.

So the derivative of sin(x) with respect to x is cos(x). To find the derivative of cos(x), I could easily do the first principles again, but creating the images takes too long, and I need the time for the later ones. Instead, I'm going to look at this graphically, and find the derivative through that. Though I'm going to be completely honest, sin(x) and cos(x) are two that I already know from past curiosity. Now, I'm just proving them.

Below is a graph of cos(x).

As we can see, we have stationary points at kπ, where k is an integer. It's at these points where the derivative will be 0. From there, the function goes from decreasing to increasing then from increasing to decreasing between the stationary points. We have points of inflection at (2k+1)π/2, where k is an integer. It's at these points where we will have a maximum or a minimum. Below shows the graph of what the derivative really looks like, as well as the actual function.

So we can see that the derivative of cos(x) is -sin(x). Next, we can move onto the fun ones, starting with tan(x). We can change this using the following trigonometric identity.

And we know that we can use the quotient rule, which states the following. Luckily, we know what each of these is.

This can be rearranged to get rid of that double negative.

This is turning out much nicer than I thought it would. We can apply a trigonometric identity, since cos²(x)+sin²(x)=1.

And finally, we can simplify.

So now we have the basic 3 trigonometric functions and their derivatives:

Original -> Derivative

sin(x) -> cos(x)

cos(x) -> -sin(x)

tan(x) -> sec²(x)

In my next blog post, I will continue to find the remaining derivatives of trigonometry.