Background: Some integrals are impossible to complete in the format they're given in. For example, the following:
If we tried integrating this with respect to x first, we'd probably start by doing a u-substitution of u = x2. The issue is: du = 2x*dx. This doesn't exist, and we run into a brick wall.
Fubini's Theorem states the following is true (Thank you, Wikipedia):
If the 3y was replaced with a numerical value, there wouldn't be a problem. However, the problem is: we have a variable as one of our bounds. If we flip the integration without changing anything, we'd end up with an function of y instead of a constant value.
It's also important to note exactly what we're doing here. In a single integral, we're finding the area under a curve. In a double integral, we're given a function of f(x,y). Finding the double integral of this function gives us the volume of the function in the given bounds. The function, as it's given, looks like this:
Usually, I'd be using the Desmos graphing calculator, but that's incapable of graphing 3D functions, so instead, I'm using Geogebra.
This is what the function looks like while bounded. The red axis is the x axis, the y axis is green (which you can hardly see through the green function), and the z axis is the blue axis. The green surface is the function we're trying to integrate in the region enclosed by the blue planes. Specifically, the centered triangle.
In order to switch the integration bounds, we actually need to find new bounds altogether, starting with dy (green) then integrating over dx (red) after. In order to be able to do this, we actually need to now write y was a function of x, since we want to be able to introduce an x into the integral but out of the exponent. In doing so, the function will capable of being integrated with respect to x, since doing a u substitution would make a valid statement.
The initial bounds, as defined in the original integral, are:
x ∈ [3y, 9]
y ∈ [0, 3]
Being able to see the actual function helps me know somewhat what I need to do: Find each corner of the integrating region and rewrite the integral.
The red region is the area we're integrating over. The edges exist at (0,0), (9, 0) and (9, 3). Now, we just need the regions. First, let's start with what we want. We want dy first, which means the long side of the rectangles are going to be from left to right. So our bounds are going to be top-down. The lower bound should be 0, because this is along the x axis. The upper bound should just be a function in terms of x. Since we know the original integral says "x = 3y", we can just solve for y: "y = x / 3". This becomes our upper bound.
The bounds for x are simpler to make, since those are just numerical values. The minimum is 0 and the maximum is 9. Therefore, those are the bounds. Now that we have the bounds, we should be able to integrate this normally.
Now, we can apply the proper u-substitution.
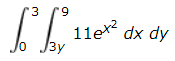









No comments:
Post a Comment